2005年大検数学解答　　 　ｍｅｍｏ()

---

mail to: adrs		前年	次年
Last update: 2005/10/10 　　　　 　(05/10/07作成)

---

[１]１．（２ａ＋ｂ＋ｃ)² を展開すると
　　　　　 [ア]a²＋b²＋c²＋[イ]ab＋[ウ]bc＋[エ]ca
　 [解]　＝[４]a²＋b²＋c²＋[４]ab＋[２]bc＋[４]ca
　考え方としては (Ａ＋Ｂ)²＝Ａ²＋２ＡＢ＋Ｂ² より、(ｂ＋ｃ)を Ｂ と考えれば
　　与式＝４ａ²＋４ａ(ｂ＋ｃ)＋(ｂ＋ｃ)²　　　　　　　(末項２乗項に再適用)
　　　　＝４ａ²＋４ａｂ＋４ａｃ＋ｂ²＋２ｂｃ＋ｃ²
　　　　＝４ａ²＋ｂ²＋ｃ²＋４ａｂ＋２ｂｃ＋４ｃａ

[１]２．　６ｘ²−ｘ−２　を因数分解すると
　　　　([オ]ｘ＋[カ])([キ]ｘ＋[ク])
　[解]＝([２]ｘ＋[１])([３]ｘ−[２])
　(別解：根の公式：時間が掛かるが、答えは出る)
　式の値を０として、根を求めると、
　ｘ＝｛−B±√(B²−４AC)｝／2A だから
　ｘ＝｛−(−１)±√(１−４×６×(−２))｝／(２×６)
　　＝(８　or　−６）／１２
　　＝２／３　or　−１／２
∴与式＝６(ｘ＋１／２)(ｘ−２／３)
　　　＝(２ｘ＋１)(３ｘ−２)

[１]３．　√２／(√３＋√２)　は、分母を有理化すると　√ケ−コ　になる．
　[解]：ａ²−ｂ²＝(ａ＋ｂ)(a−ｂ)　の関係を利用して分子・分母両方に
　　　(√３−√２)を乗ずると、与式＝√２(√３−√２)／（３−２）＝√６−２
　　　となります。ケ：６、コ：２。

　「有理化」というのは有理数に変えること。分母が√ｎなら、分子・分母双方に√ｎを掛けて（＝×√ｎ／√ｎ）を掛ければ、分母は有理数ｎに変わるが、分母が例題のように和の場合には (ａ＋ｂ)(ａ−ｂ)＝ａ²−ｂ² を利用して、分子・分母に片方の無理数項の符号が逆の値を掛けることで有理化する
　分母に無理数があると桁数が多くて近似値計算が大変だが、有理数に変換できると算出が楽になる。
　物理の単位系で「＊＊＊有理単位系」というのは、全空間の立体角：４πで湧きだし量を割って、１立体角(ステラジアン：１ｍ離れた点で１ｍ²となる)当たりの値で定義するものを言う。例：Iカンデラの光源からは４πIルーメンの光束が発せられ、１ｍ地点の光束密度＝照度はIルックス(＝４πI／４π)である。電気系はＭＫＳＡ有理単位系≒ＳＩ：国際単位が主。ガウスとかエルステッドは使えないことになっている、が、磁性材料分野で死滅していない。

[２]１．一次不等式　２ｘ−３≧４ｘ＋５　の解はどれか。番号を選べ。
　[解]　左右両辺から　２ｘ＋５を引くと　−８≧２ｘ、
　　　左右両辺を２で割ると　−４≧ｘ、
　　　すなわち　ｘ≦−４　の項番が正解。ア：「２」

[２]２．二次方程式　２ｘ²−５ｘ−１＝０　の解は
　[解]　ｘ＝{−(−５)±√(５²−４・２(−１))}／(２・２)
　　　　　＝{５±√(25＋８)}／４
　　　　　＝{５±√(３３)}／４
　　　　　＝{イ±√(ウエ)}／オ　　　　である。

[２]３．　１個６０円のリンゴと、１個４０円のミカンを併せて25個買い、合計の代金を1250円以内にしたい｡このとき、リンゴは[カキ]個まで買うことができる。
　[解]　６０林檎＋４０蜜柑≦1250円　……(1)
　　　　林檎＋蜜柑＝２５　…………………(2)　だから
　　　　蜜柑＝２５−林檎　…………………(3)　を(1)に代入
　　　　６０林檎＋４０(２５−林檎)＝２０林檎＋１０００≦１２５０
　　　　２０林檎≦２５０
　　　　　　林檎≦１２．５　従って林檎は最大１２個、[カキ]＝[１２]

[２]４．正方形の土地がある。この土地の縦の長さを１ｍ長くし、横の長さを３ｍ短くして長方形にしたら、その面積が60ｍ²になった。このとき､もとの土地の一辺の長さは[ク]ｍである
　[解１]　(ク＋１)(ク−３)＝６０　が出題だから、整理すると
　　　ク²−２ク−６３＝０＝(ク−９)(ク＋７)　……因数分解法
　　　二次方程式の根としては　ク＝９ or −７　だが負の辺長はあり得ないから
　　　ク＝９ｍ　となる。
　　　(変数名は本当はアルファベットx,y,z……にこだわる必要はない)
　[解２：根の公式による因数分解法]　解が閃けば直接因数分解した方が早いのだが
　　ク＝{−(−１)±√(１²−１・(６３))}／１
　　　＝１±√６４＝９ or −７、前解同様負長は不適につきク＝９ｍ

[３]１．二次関数　ｙ＝−(ｘ＋３)² の概形として、最も適当なものはどれか｡番号を［ア］へ記入せよ｡
　[解]　(1)係数が負なので上に凸、(2)ｘ＝−３で頂点、(3)そのｙ座標は０。この３つの条件を満たすグラフは[３]のみ。[ア]＝[３]

[３]２．二次関数 ｙ＝ｘ²−４ｘ のグラフの頂点の座標は（[イ]，[ウエ]）である。
　[解１]　軸のｘ座標＝−B／２A＝−(−４)／(２)＝２。
　　　　このときのｙ座標は２²−４・２＝−４。
すなわち（[イ]，[ウエ]）＝（[２]，[−４]）
　[解２]　ｙ＝ｘ（ｘ−４）だから、ｘ＝０，４がｘ切片だから、
　　　　ｘ＝２が対照軸の座標で、ｘ＝−４となる。
すなわち（[イ]，[ウエ]）＝（[２]，[−４]）

[３]３．二次関数 ｙ＝ａ(ｘ−２)²＋３ (ａは定数)のグラフが
　　　（１，５）を通るとき，ａの値は[オ]である。
　[解]　題意より　５＝ａ(１−２)²＋３
　　　　即ち､ａ＝２＝[オ]

[４]１．二次関数 ｙ＝(ｘ−１)²＋４ において、ｘの変域を −１≦ｘ≦２ とする
　　　とき、ｙの変域は [ア]≦ｙ≦[イ] である｡
　[解]　二次の係数が正なので下に凸で、対照軸のｘ座標はｘ＝１ なので指示されたｘの変域中のｘ＝１に頂点(最小値)が存在し、変域両端(−１ or ＋２)のどちらかが最大値だが、ｘ＝１からの距離はｘ＝−１の方が大きいから、こちらで最大値となり、その値は　(−１−１)²＋４＝８、すなわち　[ア]≦ｙ≦[イ]　は　[４]≦ｙ≦[８]　となる。
　境界２については直接計算しても可。ｙ(２)＝５　だから変域の中間値になり境界値ではない。

[４]２．二次関数　ｙ＝ｘ²＋10ｘ＋ｋ　(kは定数)のグラフがｘ軸と接するとき、
　　　ｋの値は[ウエ]である
　[解]　判別式＝０　がキー。５²−ｋ＝０、ｋ＝２５＝[ウエ]

[４]３．右の図は、二次関数 ｙ＝−ｘ²＋９ のグラフである。
　　　二次不等式　−ｘ²＋９＜０　の解はどれか。
　[解]　ｙ＝−(ｘ−３)(ｘ＋３)　だから、二次係数が負で上に凸で、ｘ切片(ｙ＝０のｘ座標)はｘ＝±３、ということは−３〜＋３の間は上に凸で正だから範囲外、従って
　　ｘ＜−３、または　３＜ｘ　が正しい。これは[３]項。

三角比表

角度		正弦 sin	余弦 cos	正接 tan
16°		0.2756	0.9613	0.2867
17°		0.2924	0.9563	0.3057
18°		0.3090	0.9511	0.3249
19°		0.3256	0.9455	0.3443
20°		0.3420	0.9397	0.3640

[５]１．Ａ地点とＢ地点の間をケーブルカーが運行している。Ａ地点とＢ地点の間の線路に沿う距離は1000ｍ、Ａ地点とＢ地点の間の高低差は300ｍであった。下の図はその様子を表したものである｡
　このとき、水平面に対するこの斜面の傾斜角の大きさは(1)〜(4)のうち､どの範囲に有るか｡最も適当なものを選べ。[ア]（see 三角比表）
　(1)．16度≦＜17度
　(2)．17度≦＜18度
　(3)．18度≦＜19度
　(4)．19度≦＜20度

　[解]　sin勾配角＝300／1000＝0.3000　だから、三角比表より、18度弱の17度台で有ることがわかり、範囲を示す不等号により(2)が正答である。
　土木・建築での勾配は通常、高低差を水平距離で割った正接で表すから、正弦での出題が落とし穴になっていることに注意。正弦は勾配抵抗である。

[５]２．cos160度は(1)〜(4)のうちどれか､最も適当なものを一つ選べ。
　(1)．　0.3420
　(2)．−0.3420
　(3)．　0.9397
　(4)．−0.9397
　[解]　cos(θ)＝−cos(180−θ) ∴
　　cos(160)＝−cos(180−160)
　　　　　　＝−cos(20)＝−0.9397
　　これは(4)である．

[６]１．tan135°の値は(1)〜(4)のうちどれか､正しい番号を一つ選べ。[ア]
　(1)．　１／√２
　(2)．−１／√２
　(3)．　１
　(4)．−１

　[解]　tanθ＝−tan(180−θ)　だから
　　tan135°＝−tan(180−135)
　　　　　　＝−tan(45)＝−１
　　　従って(4)

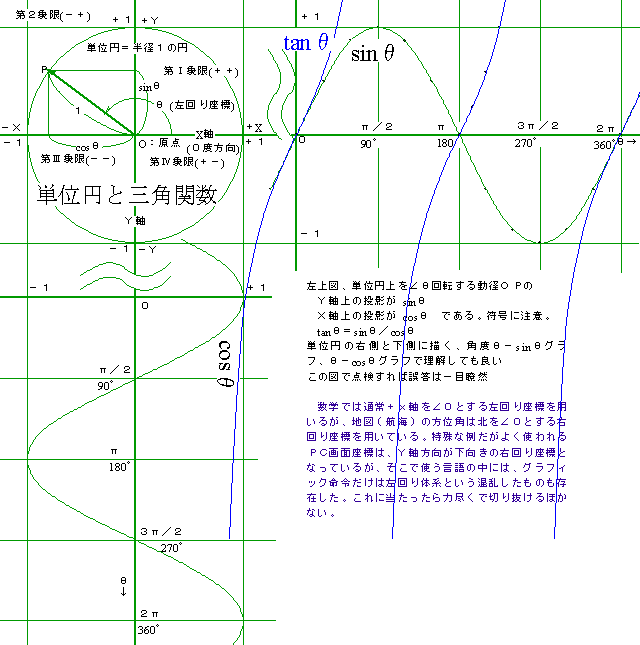
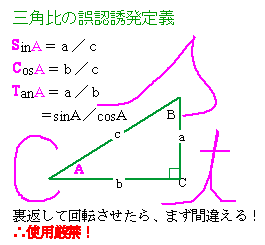　２〜４象限(90度〜360度、0度〜−270度：例題５．２　＆　６．１)の三角比をミスせず第１象限(０度〜90度)の値に換算するには、換算式丸覚えだけでなく、連続波形方式と単位円動径投影方式(右上図)の３通りが考えられる。正しく算出できればどれでも良いので、各自の感覚に合う方式で記憶されたい。時折初級の参考書に見掛ける筆記体のｓ、ｃ、ｔ方式(右図)では裏返しただけで間違えるので絶対避けること。

[６]２．角Ａが鋭角で、cosＡ＝３／４ のとき，sinＡの値は √[イ]／[ウ] である。
　[解]　sin²Ａ＋cos²Ａ＝１ より,
　　　sinＡ＝√{１−cos²Ａ}
　　　　　 ＝√{１−(３／４)²}
　　　　　 ＝√７／４
　　鋭角：90度未満、鈍角：90度超〜180度未満

[６]３．右の図の三角形ABCにおいて､AB＝２√２cm、AC＝１cm、∠A＝45°である。
　　　このとき､BCの長さは√[エ]cmである｡
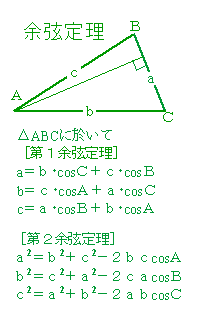　[解]　第二余弦定理(右下図)により
　　　ｂ²＋ｃ²−２ｂｃ・cosＡ＝ａ²　だから
　　 BC²＝(２√２)^2＋１−２・２√２・１・cos45°
　　　　＝８＋１−４√２・１・／√２
　　　　＝９−４√２・１・／√２＝５
　　　BC＝√５ cm　　(負は辺長につき不適)

[６]４．右の図の三角形ABCにおいて、
AB＝３cm、AC＝２cm、∠Ａ＝120°であるとき、三角形の面積は　([オ]√[カ])／[キ] cm²　である。
　[解]　sin120°＝sin60°＝√３／２　だから
　　　三角形の面積＝（１／２）底辺×高さ
　　　　　　　　　＝（１／２）３・２{√３／２}
　　　　　　　　　＝３√３／２ cm²

[６]５．右の図のように、相似な二つの円錐形の容器Ｐ、Ｑがある｡容器Ｐの底面の直径は５cm、容器Ｑの底面の直径は１５cmである。容器Ｐにいっぱいに水を入れて、容器Ｑに水を移し替えることを繰り返すとき、丁度[クケ]回で容器Ｑがいっぱいになる。（図は自明につき省略）
　[解]　相似立体の体積比は、寸法比の３乗だから、
　　　　[クケ]＝(１５／５)³＝３×３×３＝[27]倍
　[解’]　相似円錐の体積比は、まず底面積比が寸法比の２乗で、高さが寸法比だから、寸法比の３乗倍になる。すなわち、
　　　　[クケ]＝(１５／５)³＝３×３×３＝[27]倍