MTM 05/08Ａ等級昇格試験　　 　ｍｅｍｏ()

[問１]．縦が15ｍ、横が18ｍの土地に、下図のように同じ幅の道を付けたところ、道の部分を除いた土地の面積が180ｍ²になった｡(土地と道は総て直交)。このときの道の幅を求めよ。
　[解]　道幅をＷとすれば、題意は　(18−Ｗ)(15−Ｗ)＝180ｍ² で、Ｗの条件としては 0≦Ｗ≦15 となるから、式を展開すると
　　　Ｗ²−33Ｗ＋270＝180　すなわち
　　　Ｗ²−33Ｗ＋ 90＝０　となる
　　因数分解から求めると　(Ｗ−3)・(Ｗ−30)＝０　だから
　　　Ｗ＝３ or ３０ だが、初期の条件より30＞15≧Ｗなので解30は捨てられ
　　　Ｗ＝３ｍ となる。
　　解の公式で根を求めると
　　　Ｗ＝{−(−３３)±√(３３²−４・１・90)}／２
　　　　＝{３３±√(１０８９−３６０)}／２
　　　　＝{３３±√(７２９)}／２
　　　　＝{３３±２７}／２
　　　　＝３ or ３０　で、同様にＷ＝３ｍとなる。 (閃けば因数分解法の方が速い)

[問２]．次の二次関数の最大値と最小値を求めよ。
　　ｙ＝２(ｘ＋１)²＋４　　(−２≦ｘ≦１)
　[解]　２次の係数が正なので下に凸、対称軸のｘ座標は ｘ＝−１ で範囲内。従って、ｘ＝−２、−１、１ の場合のｙの値を求めれば判る。
　　　ｙ(−２)＝６
　　　ｙ(−１)＝４　　……最小値
　　　ｙ(＋１)＝１２　……最大値

[問３]．次の二次関数の最大値と最小値を求めよ。
　　ｙ＝−ｘ²＋３ｘ　　(−１≦ｘ≦＋１)
　[解]　２次の係数が負なので上に凸、対称軸は −３／(−２)＝1.5 で範囲外。
　　　従って、ｘ＝−１、＋１ の場合のｙの値を求めれば最大・最小が判る。
　　　ｙ(−１)＝−４　……最小値
　　　ｙ(＋１)＝＋２　……最大値

[問４]．二次関数 ｙ＝ｘ²＋６ｋ−ｋ のグラフがｘ軸と接するｋの値を求めよ。また接点の座標も求めよ。
　[解]　判別式Ｄ＝{０−４×５ｋ}＝0 で重根となり接するから、ｋ＝０
　[別解：問題式が誤植の疑い]　ｙ＝ｘ²＋６ｘ−ｋ ではないか？∵正解がｋ＝−９と発表されている。誤植として解くと
　　　判別式Ｄ＝３²−(−ｋ)＝０　　従って
　　　ｋ＝−９　で接する。

[問５]．次の直角三角形ＡＢＣについて、sinＡ、cosＡ、tanＡ、を求めよ。
　　∠Ｃが直角、辺ＡＣ＝２、辺ＢＣ＝６
　[解]　まず直角三角形の斜辺ＡＢ²＝２²＋６²＝４０　　∵三平方の定理に依る
　　　∴辺ＡＢ＝√４０＝２√10 となる。
　　　∴sinＡ＝６／２√10＝３／√10
　　　　cosＡ＝２／２√10＝１／√10
　　　　tanＡ＝６／２＝３
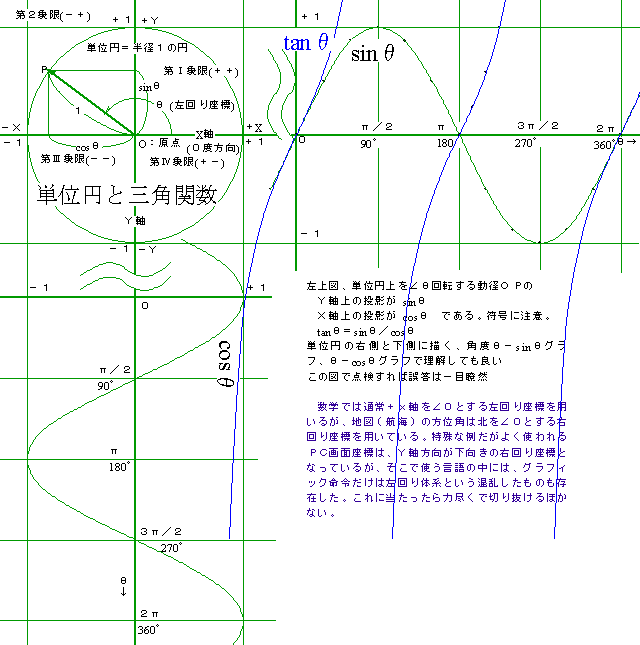[問６]．次の三角比の値を求めよ
　　　(1)．sin 150°
　[解]　与式＝sin(180°−150°)
　　　　　　＝sin 30°＝１／２
　　　(2)．cos 135°
　[解]　与式＝−cos(180°−135°)
　　　　　　＝−cos 45°
　　　　　　＝−１／√２
　[問５〜６]の単純な三角比問題５題だけで足切り点10点を確保できる！確実に解くこと。右図参照。

[問７]．生徒50人に聞いたところ、サッカーの好きな生徒が36人、野球の好きな生徒が28人、どちらも好きでない生徒が９人であった。サッカーと野球の両方とも好きな生徒は何人か？
　[解]　両方好きな人数をｘとすれば、３６＋２８＋９＝５０＋ｘ なので、ｘ＝２３人
　図を描けば一目瞭然。両方に好きだと言った分が２重計上されて総勢５０人を超える。

[問８]．６人をＡ、Ｂ、Ｃ、の３組に分ける方法は何通りあるか？
　Ａ、Ｂ、Ｃそれぞれに意味があるのかないのか？（巨人、阪神に組み分けされるのか、単なる同格の群か？）また、それぞれ１名分割を認めるのか、認めないのかなど様々な条件があり結論が異なるが、これに触れてない問題は解が何通りにもなって出題不適切。
　[解]条件：Ａ、Ｂ、Ｃ同一＝区別なし
　　●４，１，１ と分ける場合：
　　　₆Ｃ₄・₂Ｃ₁・ ₁Ｃ₁ ＝(6・5・4・3／4！)(2・1／1)(1・1／1)＝30通り
　　●３，２，１ と分ける場合：
　　　₆Ｃ₃・₃Ｃ₂・ ₁Ｃ₁ ＝(6・5・4／3！)(3・2／2)(1・1／1)＝60通り
　　●２，２，２と分ける場合：
　　　₆Ｃ₂・₄Ｃ₂・ ₂Ｃ₂ ＝(6・5／2)(4・3／2)(2・1／2)＝90通り
　　∴「組」に１個配置を含めれば 180通り。（各班同数２個なら90通り）
　[解]条件：Ａ、Ｂ、Ｃは別物
　　Ａ：Ｂ：Ｃの並び方が３！個あるので、６倍、すなわち、各班に区別のない場合で、1080通り、或いは各班各同数２個なら540通り。
　　出題不適切：解答が４通りにもなる試験問題は適切でない。

[問９]．1，1，1，2，2，3の６個の数字を使ってできる６桁の整数の個数を求めよ。
　[解]　６要素の非重複順列だが、同じものがそれぞれ３、２個存在し、その分を除くから、個数＝₆Ｐ₆／(₃Ｐ₃・₂Ｐ₂)＝６・５・４／２＝６０通り

　[別解]　１個の3が、残り5個に入る入り方は、両端があるので６個所ある。
　　　残り５個並び中から２個所を２にする(残り３個所は１)選び方は
　　　₅Ｃ₂＝５・４／２＝10通り
　　　従って、合計は６・１０＝６０通りの並び方がある

---

mail to: adrs
Last update: 2005/10/08 　　　　 　(05/10/02作成)