'03年１回再試数学２Ａ解答

---

mail to: adrs		前年２		同年１	次年２
Last update: 2005/10/22 　　　　 　(05/07/07作成)

---

【共通問題】
[１]１．８^(3/2)×(１／√２)の値は[アイ]である。
　[解]：８^(3/2)＝√(８×８×８)＝√(２³³)＝√(２⁹＝２⁴・√２)だから
　　　与式＝２⁴・√２×(１／√２)＝１６＝[アイ]

[１]２．　log₅75－(1/2)log₅９の値は[ウ]である。
　[解]：(1/n)log_aＸ＝log_aＸ^(1/n) だから
　　　(1/2)log₅９＝log₅９^(1/2)＝log₅３
　　　∴与式＝log₅75－log₅３ ＝log₅{(５²×３)／３}＝２＝[ウ]

[１]３． tan(－405°)の値は[エオ]である
　[解]：tan は180度毎の周期函数なので、360度～540度を加算しても同値。
　　∴tan(－405°)＝tan(－45°)＝tan(135°)＝－１＝[エオ]
　　　　　【参考図】 tan θ　参照


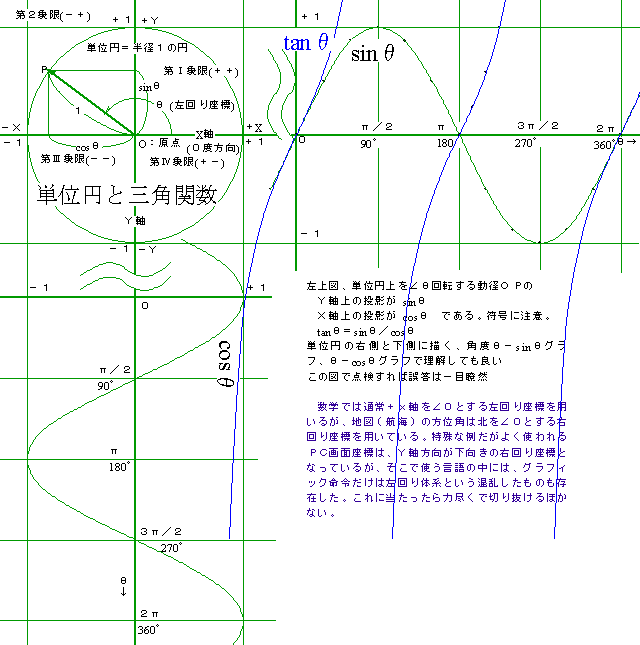
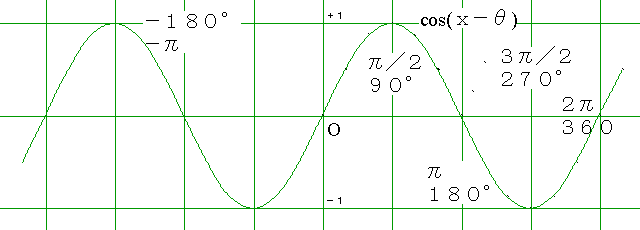
[１]４．下のグラフは、函数 ｙ＝ｃｏｓ ｘ のグラフを ｘ 軸方向に平行移動したものである。この曲線をグラフとする函数として適当なものを次の(1)～(4)から１つ番号を選べ
（出題グラフは正弦波で、90度で１，０度で０を通り、０度～90度で１／４波長である）
　[解]：cos（90度＋Ｘ₀)＝１ だから、90度＋Ｘ₀＝０
　即ち､Ｘ₀＝－90度。ｙ＝cos（ｘ－90度)　…………(ｘ＝90度で１：(3))
　　　(1)．　ｙ＝cos（ｘ＋90度)
　　　(2)．　ｙ＝cos（ｘ＋180度)
　　◎(3)．　ｙ＝cos（ｘ－90度)
　　　(4)．　ｙ＝cos（180度－ｘ)


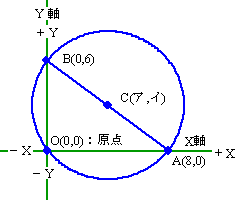[２]座標平面上に３点Ａ(8,0)、Ｂ(0,6)、Ｃ(0,0) がある。このとき次の(1)～(4)の各問に答えよ。
　[問]１．：線分ABの中点の座標は(ア,イ)である。
　　[解]１．：中点のｘ座標は　(8＋0)／２＝４、
　　　ｙ座標は　(0＋6)／２＝３
　　　即ち(４,３)である。

　[問]２．：２点AB間の距離は［ウエ］である
　　[解]２．：３平方の定理より、AB²＝BO²＋AO²、BO＝６，AO＝８ だから、
　　AB²＝６²＋８²＝１００
　　AB＝√１００＝１０＝[ウエ]

　[問]３．：直線ABの方程式は ｙ＝[オカ]／[キ]・ｘ＋[ク] である。
　　[解]３．：勾配＝(0－6)／(8－0)＝－３／４、ｙ切片＝６だから方程式は
　　ｙ＝[－３]／[４]・ｘ＋[６]

　[問]４．：３点ＡＢＯを通る円の方程式は
　　　(ｘ－[ケ])²＋(ｙ－[コ])²＝[サシ]　である。
　　[解]４．：∠AOB＝∠Ｒ：直角　だから、ΔAOBは直角三角形で、その斜辺は外接円の直径である。（直径を見込む角＝直角）。従って辺AB(＝外接円直径)の中点が外接円の中心である。その座標は(1)で求めた通りで、直径が(2)で求めた１０ なので、半径は５、半径²＝２５。
　　∴求める円の方程式は
　　　　(ｘ－[４])²＋(ｙ－[３])² ＝[２５]

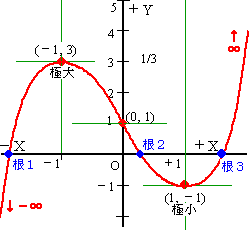[３]．函数 ｙ＝ｘ³－３ｘ＋１ について、次の(1)～(3)の各問に答えよ。
　[問]１．：導関数 ｙ’ を求めると、
　ｙ’＝[ア]ｘ²－[イ] になる｡
　　[解]１：そのまま微分して
　　ｙ’＝[３]ｘ²－[３]

　[問]２．：この函数は ｘ＝[ウ]のとき極小となり、極小値は[エオ]である。
　　[解]２：導関数が０になる点が
　　　　極値(極大＆極小)。
　　その点の第２導関数が負で極大、正で極小と判断できるから解１の結果より
　　ｙ’＝３ｘ²－３＝３(ｘ²－１）＝０、∴ｘ＝±１で極値
　　ｙ''＝６ｘ で、ｙ''(＋１)＝＋６＞０　：＋１で極小、
　　ｙ''(－１)＝－６＜０ なので、－１で極大
　　極小値は ｙ(＋１)＝(＋１)³－３(＋１)＋１＝－１
　　極大値は ｙ(－１)＝(－１)³－３(－１)＋１＝＋３
　　ｘ＝[１]のとき極小となり、極小値は[－１]である。

　[問]３．：この関数のグラフとｘ軸との共有点のうち、
　　　そのｘ座標が正であるものは[カ]個ある
　　[解]３：「ｘ軸との共有点」とはｙ＝０の点であり３次方程式の解を求めている。
　　　３次方程式の一般解はないが、３次の係数の正負で全体の勾配の正負が決まり、
　　　根(解)の個数は１～３個で、その範囲の正負を聞いているので、
　　　ｘ＝０のときの関数の正負が判ると３点と±∞の正負が判る。
　　ｙ(0)＝＋１ だからグラフの概形は、
　　ｙ(－∞)＝－∞、ｙ(－１)＝＋３、ｙ(０)＝＋１、ｙ(＋１)＝－１、ｙ(＋∞)＝∞
　　の略図から、交点＝根は負側に１，正側に２個、[カ]＝[２]個となる｡

[４]１．不定積分∫(－9ｘ²＋６ｘ－２)dx を求めると、
　　　　　　　[アイ]ｘ³＋[ウ]ｘ²－[エ]ｘ＋Ｃ　　(但し、Ｃは積分定数)
　[解]：与式＝[－３]ｘ³＋[３]ｘ²－[２]ｘ＋Ｃ

[４]２．定積分 ∫³_－3(ｘ²＋１)dx を求めると[オカ]になる｡
　[解]：与式＝[(1/3)ｘ³＋ｘ]³_－3 ＝[９＋３]－[－９－３]＝２４＝[オカ]

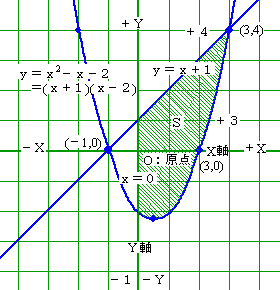[４]３．右の図は放物線 ｙ＝ｘ²－ｘ－２ と、
　　　　直線　ｙ＝ｘ＋１
　　　　を示したものである｡
　　　　　放物線と直線およびｙ軸で囲まれた斜線部(ｘ≧0)の面積をＳとするとき、次の(1)～(4)のうちから適当なものを選べ。番号[キ]
　　　　　(1)．Ｓ＝∫₀³(ｘ²－１)dx
　　　　　(2)．Ｓ＝∫₀³(－ｘ²＋１)dx
　　　　　(3)．Ｓ＝∫₀³(ｘ²－２ｘ－３)dx
　　　　　(4)．Ｓ＝∫₀³(－ｘ²＋２ｘ＋３)dx
　[解]：題意の２次式のグラフと直線との交点では、両方のｘ、ｙの値が等しいから
　　　ｘ²－ｘ－２＝ｘ＋１
　　　即ち ｘ²－２ｘ－３＝０
　　　因数分解すると (ｘ＋１)(ｘ－３)＝０ だから、ｘ＝－１、ｘ＝３ で交わる。
　　（又は根の公式より ｘ＝{１±√(１＋３×１)}／１＝３ or －１　で交わる）
　　題意から、ｘの範囲はこのうちのｘ＝０～ｘ＝３ で、
　　２次式の２次の係数が正だから下に凸。
　　∴面積を求めるには、直線から２次式を引いた値がｙの瞬時値、すなわち
　　ｙ＝(ｘ＋１)－(ｘ²－ｘ－２)
　　　＝－ｘ²＋２ｘ＋３　だから
　　面積Ｓ＝∫₀³(－ｘ²＋２ｘ＋３)dx
　　すなわち、[キ]＝[４]
　　面積計算すれば、Ｓ＝[－ｘ³／３＋ｘ²＋３ｘ]₀³
　　　　　　　　　＝(－９＋９＋９)－(－０＋０＋０）＝９　だが、
　　　　　　　　　題意は面積そのものは求めていない。

[５]１．　３ｘ²＋７ｘ－６ を因数分解すると、
　　　　([ア]ｘ－[イ])(ｘ＋[ウ])　　になる。
　[解]：([３]ｘ－[２])・(ｘ＋[３])
　　[別解]：根の公式から解くのは、面倒
　　ｘ＝{－７±√(７²－４・３・(－６))}／(２×３)
　　　＝{－７±√(４９＋７２)}／（２×３）＝{－７±√(１１²)}／（２×３）
　　　＝４／６ or －１８／６
　　　＝２／３ or －３
　　従って与式＝３(ｘ－２／３)(ｘ＋３)＝(３ｘ－２)・(ｘ＋３) 　　　

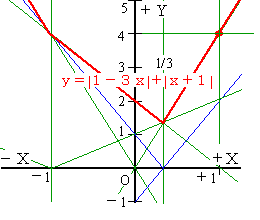
[５]２．　ｘ＝１のとき、|１－３ｘ|＋|ｘ＋１|の値を求めると、[エ]になる．
　[解]：絶対値(||)はy=0を境に極性が反転する訳だから、
　　　左辺||＝０は ３ｘ＝１、ｘ＝1/3 を境界に １＞1/3 では逆極性で ｙ＝３ｘ－１
　　　同様に右辺は　ｘ＋１＝０、ｘ＝－１を境に １＞－１ の範囲は ｙ＝ｘ＋１
　　従ってｘ＝１での原式＝(３ｘ－１)＋(ｘ＋１)＝４＝[エ]

ｙ＝|１－３ｘ|＋|ｘ＋１| の実態(cf.)

x範囲		左辺	右辺		総和:ｙ＝
x<－１		１－３ｘ	－ｘ－１	－４ｘ
－１<x<1/3			ｘ＋１	－２ｘ＋２
1/3<x		３ｘ－１		＋４ｘ

　　

[５]３．　{２＋√３}／{２－√３} は分母
　　を有理化すると[オ]＋[カ]√[キ] になる
　[解]：分母が{２－√３}だから、分子、分母双方に {２＋√３} を掛けると、
　与式＝４＋３＋４√３＝７＋４√３
　　　展開公式の、(Ａ＋Ｂ)(Ａ－Ｂ)＝Ａ²－Ｂ² を使うと分母の√をなくすことができて、数値計算が楽になる。この様に分子・分母に同数を掛けて(＝１を掛けて)分母から無理数(この場合平方根号)を無くす変換操作を「分母の有理化」という。

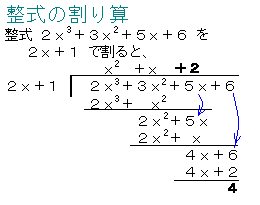[５]４．整式 ２ｘ³＋３ｘ²＋５ｘ＋６ を
　 ２ｘ＋１ で割ると、商は
　 ｘ²＋ｘ＋[ク]で、余りは[ケ]になる｡
　[解]：商：ｘ²＋ｘ＋[２]、余り[４］
　　（計算は右図）

[６]１． を計算すると
　　[アイ]になる｡
　[解]：ｋ＝１ で ２ｋ＋１＝３、
　２で５、３で７、４で９、５で１１、
　６で１３だから
　　計＝(３＋１３)×６項／２
　　　＝４８＝[アイ]
　　(Σの意味と、等差級数の和の計算)

[６]２．等差数列 58,52,46,…… がある｡
　　(1)．この数列の第ｎ項をｎの式で表すと[ウエ]ｎ＋[オカ]になる。
　　(2)．この数列において、はじめて負になる項は第[キク]項である。
　[解]：公差＝46－52＝52－58＝－６、初項58＝－６×１＋Ｃ、∴Ｃ＝58＋6＝64
　　　∴第ｎ項＝－６ｎ＋６４　……解(1)
　　　－６ｎ＋６４＜０　　 ６ｎ＞６４　　ｎ＞３２／３≒１０．６６６６
　　　ｎは整数値だから、ｎ＝１１　……解(2)

[６]３．初項が２，第４項が５４である等比数列がある。この数列の第２項は[ケ]である
　[解]：公比をａとすると、２ａ^(4-1)＝５４ だから　ａ³＝５４／２＝２７＝３³
　　∴ａ＝３＝[ケ]

[６]４．ａ₁＝１，ａ_n+1＝ａ_n＋ｎ² (ｎ＝１，２，３，４　……)　で定まる
　　数列｛ａ_n｝がある。
　　この数列の第４項は[コサ]である。
　[解]：ｎ＝１で　１項＝１
　　　　ｎ＝２で　２項＝１＋１²＝２
　　　　ｎ＝３で　３項＝２＋２²＝６
　　　　ｎ＝４で　４項＝６＋３²＝１５＝[コサ]

[７]１．
　[解]：

[７]２．
　[解]：

[８]１．
　[解]：

[８]２．
　[解]：

[８]３．
　[解]：